OpenGL教程:13. 深度测试
一般情况下,OpenGL在渲染物体的时候,总是有个“先来后到”的顺序。比如一开始渲染了三角形,后来在三角形的位置上渲染矩形,那么这个矩形就会覆盖三角形。
在三维空间也有类似的情况,比如渲染正方体,如果先渲染前面,然后渲染后面,那么后面就会覆盖前面。一个简单的解决方案就是启用深度测试。
之前,我们渲染了一个3D箱子,并且运用了深度缓冲(Depth Buffer)来防止被阻挡的面渲染到其它面的前面。在这一节中,我们将会更加深入地讨论这些储存在深度缓冲(或z缓冲(z-buffer))中的深度值(Depth Value),以及它们是如何确定一个片段是处于其它片段后方的。
深度缓冲就像颜色缓冲(Color Buffer)(储存所有的片段颜色:视觉输出)一样,在每个片段中储存了信息,并且(通常)和颜色缓冲有着一样的宽度和高度。深度缓冲是由窗口系统自动创建的,它会以16、24或32位float的形式储存它的深度值。在大部分的系统中,深度缓冲的精度都是24位的。
当深度测试(Depth Testing)被启用的时候,OpenGL会将一个片段的深度值与深度缓冲的内容进行对比。OpenGL会执行一个深度测试,如果这个测试通过了的话,深度缓冲将会更新为新的深度值。如果深度测试失败了,片段将会被丢弃。
深度缓冲是在片段着色器(fragment shader)运行之后(以及模板测试(Stencil Testing)运行之后。
屏幕空间坐标与通过OpenGL的glViewport所定义的视口密切相关,并且可以直接使用GLSL内建变量gl_FragCoord从片段着色器中直接访问。gl_FragCoord的x和y分量代表了片段的屏幕空间坐标(其中(0, 0)位于左下角)。gl_FragCoord中也包含了一个z分量,它包含了片段真正的深度值。z值就是需要与深度缓冲内容所对比的那个值。
我们一般用如下语句启用深度测试:
1 | glEnable(GL_DEPTH_TEST); |
当它启用的时候,如果一个片段通过了深度测试的话,OpenGL会在深度缓冲中储存该片段的z值;如果没有通过深度缓冲,则会丢弃该片段。如果你启用了深度缓冲,你还应该在每个渲染迭代之前使用GL_DEPTH_BUFFER_BIT来清除深度缓冲,否则你会仍在使用上一次渲染迭代中的写入的深度值:
1 | glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); |
深度测试函数
我们可以决定深度测试的“比较运算符”,来控制OpenGL在何时丢弃一个片段:
1 | glDepthFunc(GL_LESS); |
这个函数接受下面表格中的比较运算符:
| 函数 | 描述 |
|---|---|
| GL_ALWAYS | 永远通过深度测试 |
| GL_NEVER | 永远不通过深度测试 |
| GL_LESS | 在片段深度值小于缓冲的深度值时通过测试 |
| GL_EQUAL | 在片段深度值等于缓冲区的深度值时通过测试 |
| GL_LEQUAL | 在片段深度值小于等于缓冲区的深度值时通过测试 |
| GL_GREATER | 在片段深度值大于缓冲区的深度值时通过测试 |
| GL_NOTEQUAL | 在片段深度值不等于缓冲区的深度值时通过测试 |
| GL_GEQUAL | 在片段深度值大于等于缓冲区的深度值时通过测试 |
默认情况下###使用的是GL_LESS,启用之后会得到如下的场景:
如果改成GL_ALWAYS:
1 | glEnable(GL_DEPTH_TEST); |
结果就是:
后渲染的物体永远都被前面所渲染的物体所覆盖!
深度值精度
线性深度精度
深度缓冲包含了从0到1的深度值,它将会与观察者视角所看见的场景中所有物体的z值进行比较。观察空间的z值可能是投影平截头体的近平面(Near)和远平面(Far)之间的任何值。我们需要一种方式来将这些观察空间的z值变换到[0, 1]范围之间,其中的一种方式就是将它们线性变换到[0, 1]范围之间。下面这个(线性)方程将z值变换到了0.0到1.0之间的深度值:
容易证明$F_{depth}\in [0, 1]$,这是因为$z \in [near, far]$。
这里的near和far值是我们之前提供给投影矩阵设置可视平截头体的那个 near 和 far 值。这个方程需要平截头体中的一个z值,并将它变换到了[0, 1]的范围中。z值和对应的深度值之间的关系可以在下图中看到:
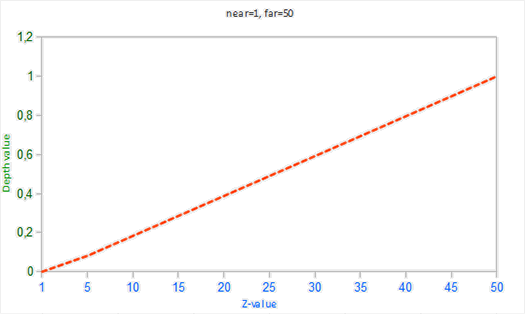
可以看到近远的深度精度都是一致的,都为线性
非线性深度精度
实际上我们更多用的是非线性深度,毕竟对于远处来说,我们没有必要用到更高的深度,因此可以用下面的函数来定义非线性深度精度:
深度缓冲中的值在屏幕空间中不是线性的(在透视矩阵应用之前在观察空间中是线性的)。深度缓冲中0.5的值并不代表着物体的z值是位于平截头体的中间了,这个顶点的z值实际上非常接近近平面!你可以在下图中看到z值和最终的深度缓冲值之间的非线性关系:
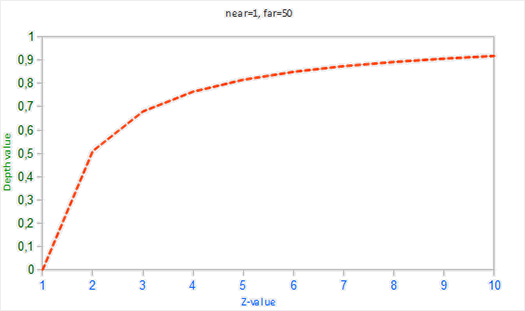
可以看到,深度值很大一部分是由很小的z值所决定的,这给了近处的物体很大的深度精度。这个(从观察者的视角)变换z值的方程是嵌入在投影矩阵中的,所以当我们想将一个顶点坐标从观察空间至裁剪空间的时候这个非线性方程就被应用了。如果你想深度了解投影矩阵究竟做了什么,我建议阅读这篇文章。
深度缓冲可视化
在前面我们说过gl_FragCoord的z分量就是片段的深度值,我们可以用利用这个向量作为颜色的输出,从而达到深度缓冲的可视化:
1 | void main() |
运行程序:

可以看到在远处我们的片段呈现白色,而近处呈现黑色。并且我们OpenGL的深度缓冲默认为非线性的!因此在足够远的情况下,这三个片段都是白色的!靠近的情况下,才有所改观(如上图),近处的物体比起远处的物体对深度值有着更大的影响。只需要移动几厘米就能让颜色从暗完全变白。
然而,我们也可以让片段非线性的深度值变换为线性的。要实现这个,我们需要仅仅反转深度值的投影变换。这也就意味着我们需要首先将深度值从[0, 1]范围重新变换到[-1, 1]范围的标准化设备坐标(裁剪空间)。接下来我们需要像投影矩阵那样反转这个非线性方程(方程2),并将这个反转的方程应用到最终的深度值上。最终的结果就是一个线性的深度值了。
因为我们的$F_{depth}\in[0,1]$,要想转换到NDC的$[-1,1]$,就需要做如下线性变换;
这是因为$2F_{depth}-1 \in [-1, 1]$.
然后根据公式1,计算: