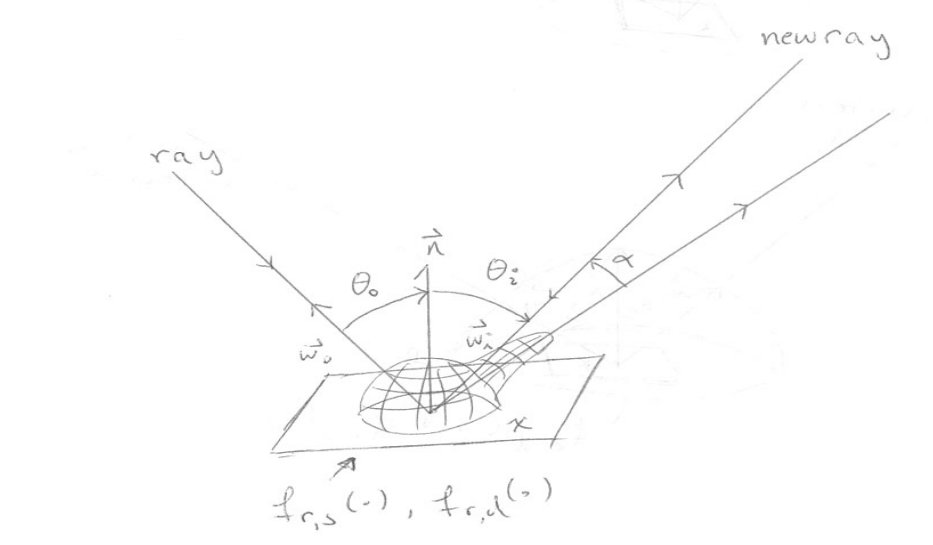
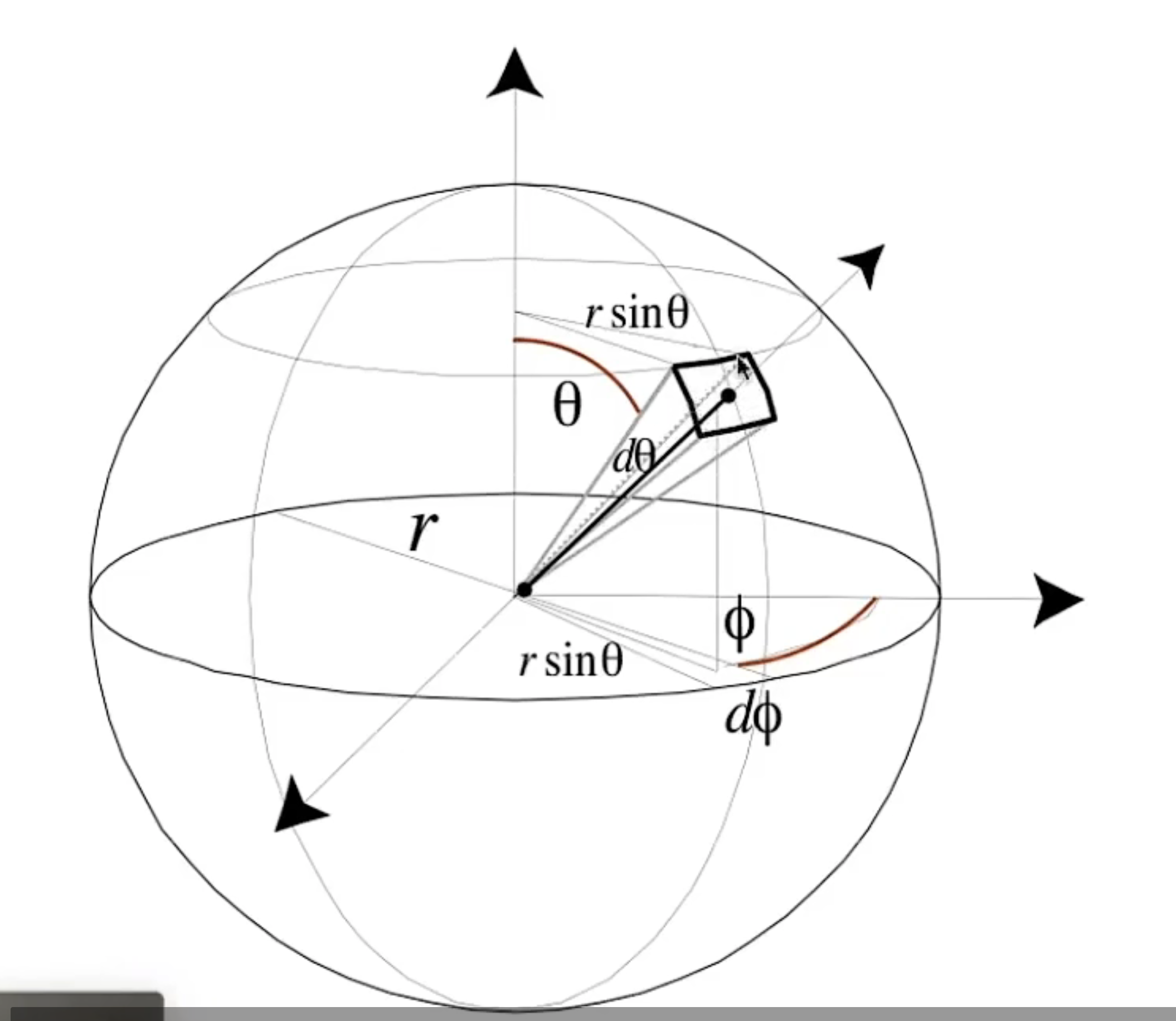
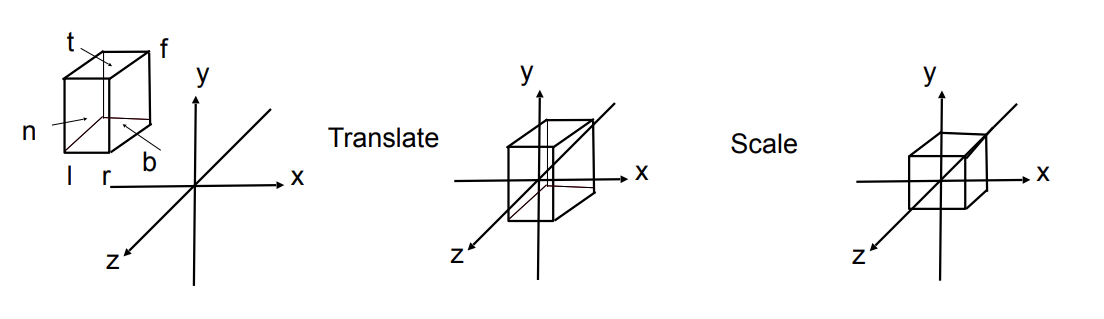
在前面介绍了BDRF函数,那么具体这个函数是什么样子的我们并不知道。接下来简单介绍常用的BRDF函数。
Phong BRDF
在学习PBR之前,我们最常用的是Phong光照模型,为了使得Phong具有物理意义,定义Phong BRDF:
- $\alpha$是光线出射方向与入射光线理想镜面反射方向之间的夹角;
- $k_d$是漫反射率(diffuse reflectivity),即投射到物体表面的能量中发生漫反射的比例;
- $k_s$是镜面反射率(specular reflectivity),即垂直投射到物体表面的能量中被镜面反射的比例;
- $n$是镜面指数(specular exponent),更高的值会产生更清晰的镜面反射;
- 为了满足能量守恒,限制$k_d+k_s\le 1$。