给定图$G=(V,E)$,其最小生成树为边权值和最小的树,并且联通了图中所有的点,设$MST$为$G$的最小生成树,那么有$MST.edgeSize=V.vertexSize-1$,意思是MST的边数一定为图中顶点数目减去1.
最小生成树常用的两种算法分别是Prim和Kruskal,这两种算法都有对应的堆优化方法,我们先从暴力的解法做起。
给定图$G=(V,E)$,其最小生成树为边权值和最小的树,并且联通了图中所有的点,设$MST$为$G$的最小生成树,那么有$MST.edgeSize=V.vertexSize-1$,意思是MST的边数一定为图中顶点数目减去1.
最小生成树常用的两种算法分别是Prim和Kruskal,这两种算法都有对应的堆优化方法,我们先从暴力的解法做起。
常见的最短路径算法一般有Floyd,Dijkstra,Johnson,Bellman-Ford算法。按照课本所学的先后顺序,我们先讲Dijkstra。
Dijkstra算法其实是Floyd的优化,成功将$O(n^3)$降到了$O(n^2)$,并且还是采用了动态规划的思想。我们从起点枚举最短路径开始。
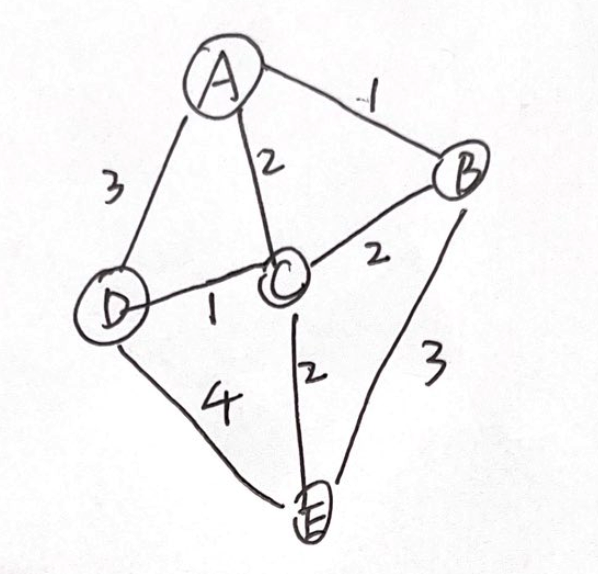
比如从A出发,我们会知道首先选择B,其路径为$A\rightarrow B:1$。好的接下来哪个路径最短?首先不能是A到D吧,边权都3了。那应该是2吗?好像是吧。。。
其实不妨这么想,在找到路径之后,都更新路径数组dp[],这里可以看到,若要A到C,可以选择$A\rightarrow C$,也可以$A\rightarrow B \rightarrow C$,但其实$A\rightarrow C$更短。
所以有了如下的状态转移方程;
其中$i$是可联通顶点,$now$是刚刚找到的最短路终顶点,$dp[i]$是起点到顶点$i$的最短路径。
Update your browser to view this website correctly.&npsb;Update my browser now