单调栈是指栈内的元素单调递增或者递减,主要是以$O(n)$的时间解决NGE问题(Next Greater Element)。就是在每个元素中,找到下一个比他大的1数。(或者其他的变式)。
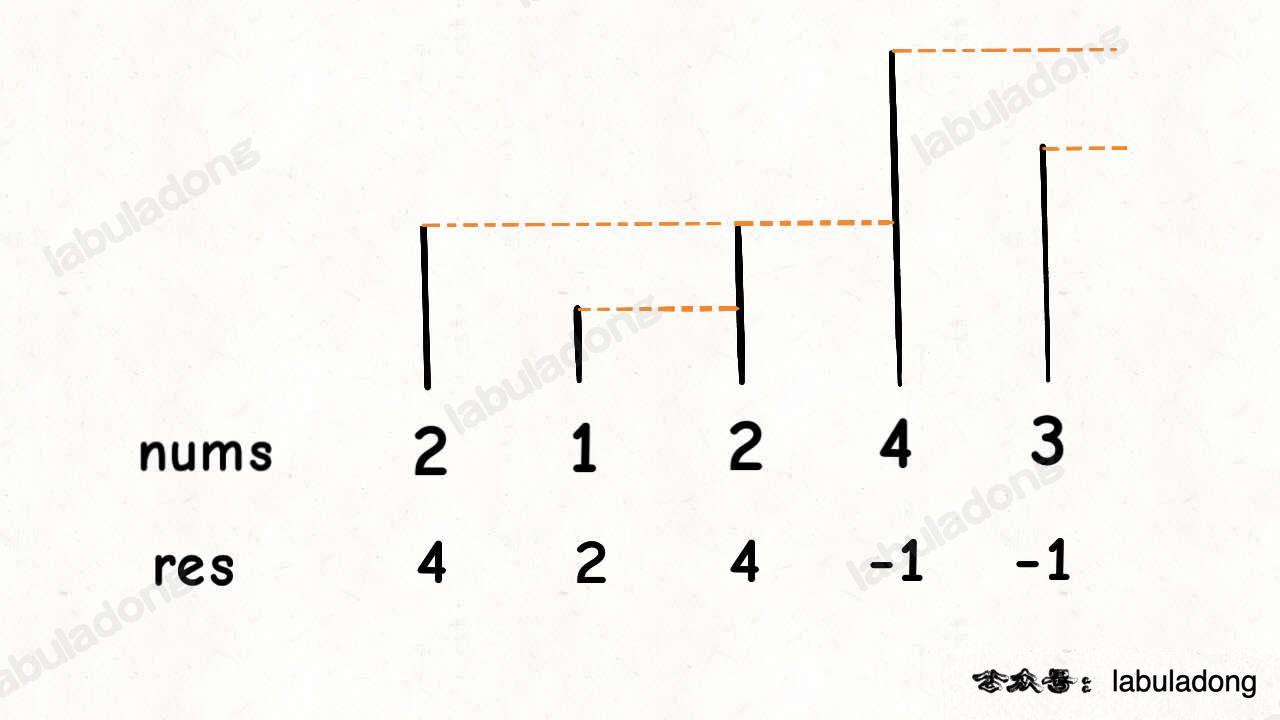
可以类似于身高,2只能看到4是第一高的,1只能看到2是第一高的…同理。
单调栈是指栈内的元素单调递增或者递减,主要是以$O(n)$的时间解决NGE问题(Next Greater Element)。就是在每个元素中,找到下一个比他大的1数。(或者其他的变式)。

可以类似于身高,2只能看到4是第一高的,1只能看到2是第一高的…同理。
单调队列稍有不同,需要用到双端队列模拟。不然的话无法正常满足单调性。
并且双端队列最好自己手写,用c++的dequeue效率非常慢,很容易tle的。
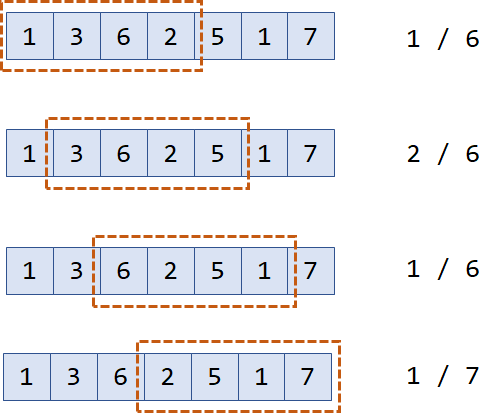
单调队列常用于解决连续k个数中的操作,比如滑动窗口问题。
并查集可以表示元素中的属于状态,比较重要。其核心元素是father数组,初始化如下:
1 | void init() { |
已知$f(x)=\frac{x^2+9}{x}\ (x>0)$,那么它的最小值为_
(利用基本不等式)
若函数$f(x)=x^2+ax^3$,当$a$为__时,函数为偶函数
奇函数:$f(-x)=-f(x)$
偶函数:$f(-x)=f(x)$
排列数:$A_n^m=\frac{n!}{(n-m)!}$
组合数:$C^m_n=\frac{n!}{(n-m)!m!}$
德·摩根律:$\overline A \cup \overline B= \overline {A\cap B},\ \overline A \cap \overline B= \overline {A\cup B}$
正态分布:$X\sim N(\mu,\sigma^2)\ \Rightarrow\ \frac{X-\mu}{\sigma}\sim N(0,1)$
$3\sigma$原则:$P(-1<\frac{X-\mu}{\sigma}<1)=0.6826$
$P(-2<\frac{X-\mu}{\sigma}<2)=0.9544$
$P(-3<\frac{X-\mu}{\sigma}<3)=0.9974$
国内的大部分教材都是通过线性相关解与线性无关解推导出齐次二阶线性微分方程的解,但大部分同学对此有些困惑,只能硬记公式。这里给出一种推导方法:
对于方程
参考一阶线性微分方程,我们不难看出$y$可以用自然数指数函数表示,因此仿照这个定义,我们令:
那么带入方程就有:
不难得出:
这个方程为微分方程的特征方程,可以知道如果我们求出$r$的两个解,那么就能求出这个微分方程。
雅可比行列式常应用于重积分的计算,对化简积分有着重大的作用,建议大家学习一下。
我们在计算重积分的时候,一般微分算子都是
或者
很多人以为这些微分算子之间是乘法运算,其实并不是。他们之间是一种楔形积的运算,记作^,因此:
或者
是他们的严格写法。
Update your browser to view this website correctly.&npsb;Update my browser now