next数组计算方法如下
默认next[0]=-1,字符串从0出发。
计算的方法是:
1 | int j = 0, k = -1; |
其中p是模式串。
接下来我们来推导KMP的状态转移方程。
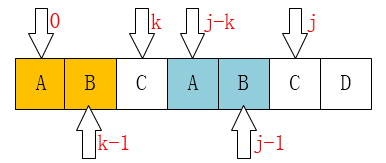
设$dp[j]$是第j处最大公共真前后缀的长度,那么如果$p[j]==p[k]$,那必然有$dp[j+1]=dp[j]+1=k+1$(可以想象一下,后面一位字符也是相等的,那就说明这里的最大公共真前后缀的长度等于前一位的+1嘛!),并且j和k都递增一次。
next数组计算方法如下
默认next[0]=-1,字符串从0出发。
计算的方法是:
1 | int j = 0, k = -1; |
其中p是模式串。
接下来我们来推导KMP的状态转移方程。
设$dp[j]$是第j处最大公共真前后缀的长度,那么如果$p[j]==p[k]$,那必然有$dp[j+1]=dp[j]+1=k+1$(可以想象一下,后面一位字符也是相等的,那就说明这里的最大公共真前后缀的长度等于前一位的+1嘛!),并且j和k都递增一次。

给定图$G=(V,E)$,其最小生成树为边权值和最小的树,并且联通了图中所有的点,设$MST$为$G$的最小生成树,那么有$MST.edgeSize=V.vertexSize-1$,意思是MST的边数一定为图中顶点数目减去1.
最小生成树常用的两种算法分别是Prim和Kruskal,这两种算法都有对应的堆优化方法,我们先从暴力的解法做起。
常见的最短路径算法一般有Floyd,Dijkstra,Johnson,Bellman-Ford算法。按照课本所学的先后顺序,我们先讲Dijkstra。
Dijkstra算法其实是Floyd的优化,成功将$O(n^3)$降到了$O(n^2)$,并且还是采用了动态规划的思想。我们从起点枚举最短路径开始。
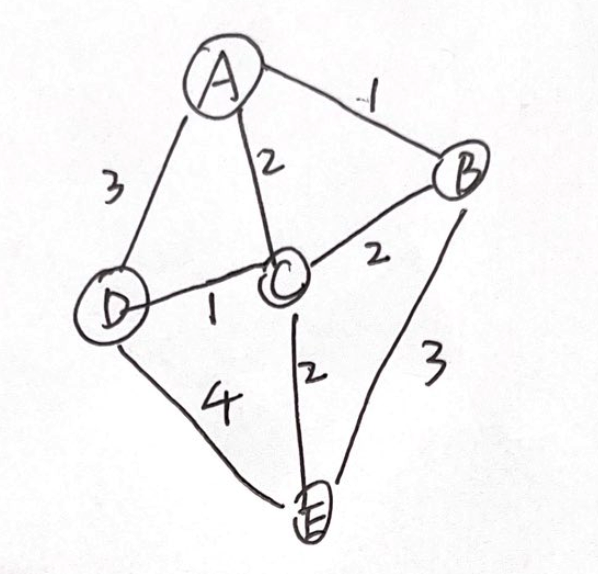
比如从A出发,我们会知道首先选择B,其路径为$A\rightarrow B:1$。好的接下来哪个路径最短?首先不能是A到D吧,边权都3了。那应该是2吗?好像是吧。。。
其实不妨这么想,在找到路径之后,都更新路径数组dp[],这里可以看到,若要A到C,可以选择$A\rightarrow C$,也可以$A\rightarrow B \rightarrow C$,但其实$A\rightarrow C$更短。
所以有了如下的状态转移方程;
其中$i$是可联通顶点,$now$是刚刚找到的最短路终顶点,$dp[i]$是起点到顶点$i$的最短路径。
哈希函数是指将任何一种类型的变量$x$映射到$hash(x)$里,其中$hash(x)$是比较小的数值。一般来说,我们希望这种函数是一对一的,但偶尔会出现哈希碰撞的情况,即一对多的情况。这种情况是不可取的。
很多情况下,我们都将字符串的起始下标设为1.
在这里,$hash(i)$表示从1到下标$i$这个字符串的哈希值。所以我们要先确定前缀字符串,比如给定:
那么$hash(0)=hash(“A”),hash(1)=hash(“AB”)…$
在计算的时候,我们把字符串当作$p$进制数,并按照ASCII码赋值,其hash函数就是将$p$进制数转换成10进制数。因此:
原理:给出中缀表达式,求出表达式的值。利用栈来模拟表达式树的操作。
比如有序列:
假如下标从1开始,让你计算区间$[a[2], a[3]]$的和。这时候数组无法简单做到,因为第二第三的数字远远超过了$10^5$,数组超过了最大的界,因此我们要做离散化。
简单来讲,比如你要有n个插入操作,每次插入提供两个值,一个是插入的位置,一个是插入的值为多少。但插入的位置可能超过$10^5$,这个时候用数组就不能统计区间和了,我们需要对这个数组进行离散化处理:

对于任何一个区间segs,我们需要将他们合并得到一个新的区间数组。比如[1, 2],[2, 3],[5, 7],[6, 9],就可以合并成[1, 3],[5, 9],合并成了两个区间。
方法其实不难,首先我们存储segs数组。然后我们将segs对x从小到大排序,这样就保证了局部有序,合并区间就不会出现缺少的情况。
接下来就是合并操作,先定义临时的区间端点st和ed。然后遍历区间数组。如果当前数组的值的x大于临时数组中的ed,那么就说明当前区间st和ed是无法继续合并的(已经最大了),所以加入到结果中。否则的话,就要更新最大的ed。
1 |
|
与单链表类似,但我们用l和r两个数组存放元素的左边和右边。
并且这次的头和尾都是固定的,不像静态单链表中头是会变化的且是存放值的。
我们设定头为0,尾为1,那么如果要删除第k位置的元素,实际上要删除下标k + 1的位置(假定位置从1开始):
Update your browser to view this website correctly.&npsb;Update my browser now