基于物理的渲染(PBR)
在前面介绍了BDRF函数,那么具体这个函数是什么样子的我们并不知道。接下来简单介绍常用的BRDF函数。
Phong BRDF
在学习PBR之前,我们最常用的是Phong光照模型,为了使得Phong具有物理意义,定义Phong BRDF:
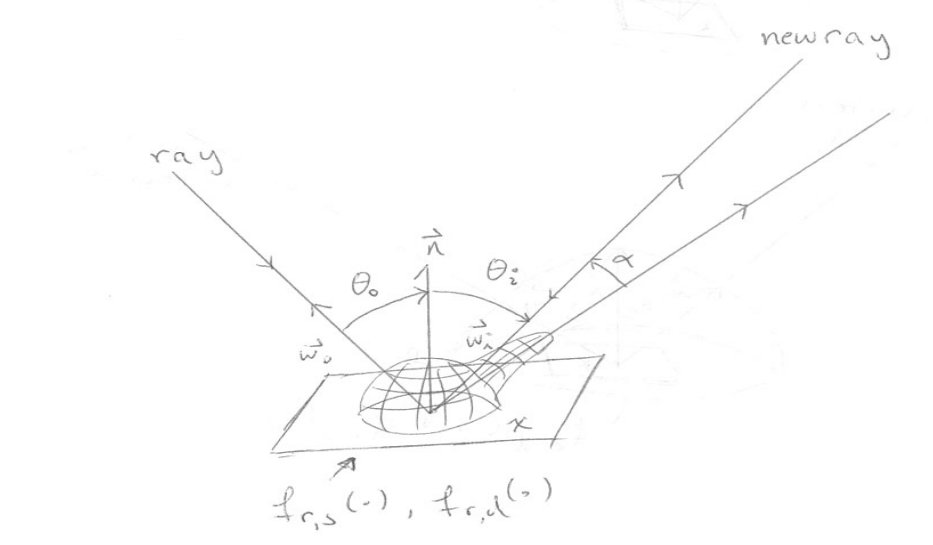
- $\alpha$是光线出射方向与入射光线理想镜面反射方向之间的夹角;
- $k_d$是漫反射率(diffuse reflectivity),即投射到物体表面的能量中发生漫反射的比例;
- $k_s$是镜面反射率(specular reflectivity),即垂直投射到物体表面的能量中被镜面反射的比例;
- $n$是镜面指数(specular exponent),更高的值会产生更清晰的镜面反射;
- 为了满足能量守恒,限制$k_d+k_s\le 1$。
Cook-Torrance BRDF
PBR渲染中使用的BRDF函数通常是Cook-Torrance提出的BRDF函数:
其中:
Lambert项:
Lambert项完全符合Lambertian漫反射光照模型,这种模型假定在所有方向观察物体表面的亮度完全相同。$f_{lambert}$中的$c$叫做反照率或者固有色。
反照率是表示光在介质内部出射部分的比例,在计算机图形学其实就是材质的颜色。
根据Lambertian漫反射光照模型,符合能量守恒定律,于是有:
由于这个模型假定在所有方向上观察物体的表面亮度完全相同,所以$f_r$是常数,因此作如下化简:
Cook-Torrance项
Cook-Torrance是一种用于渲染金属、塑料等材质的着色模型。它基于微观表面理论,将表面分解为许多微观的法向量,再根据这些法向量计算出反射光的强度。这种着色模型非常适合渲染具有粗糙表面的物体,如石头、木材、毛发等。Cook-Torrance模型将物体表面的反射光分解为漫反射光和镜面反射光两个部分,并考虑了光线在物体表面反射时的微观变化。此外,Cook-Torrance模型还考虑了物体表面的粗糙度、金属度和折射率等因素,从而能够更准确地模拟真实世界中的光照效果。
这个是PBR渲染的核心,他包括了$D$-法线分布函数,$F$-菲涅尔方程和$G$-几何遮蔽函数。
法线分布函数(Normal Distribution Function)
法线分布函数(Normal Distribution Function),是描述微平面上法线的分布的重要函数。它决定了在某个表面微区域内,法线朝向的分布情况。微平面是PBR的重要理论基础。

可以发现,在粗糙的微平面内,法向量的方向都是无序杂乱的;而光滑的微平面很多法向量的方向都是趋同的。为了能够简单计算。所以我们引入了一个粗糙度(Roughness)来表示微平面内的粗糙程度,然后基于这个粗糙度,来计算在众多微平面内趋于某个方向向量$h$的比例是多少,而这个向量其实就是半角向量(Blinn-Phong用到的那个,$l$为光线向量,$v$为视线向量):
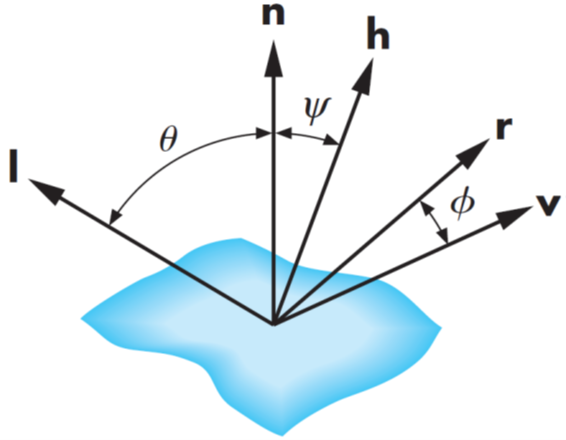
采用以半角向量为主的法线分布的原因如下:
- 表面微区域的法线方向是不连续的:表面微区域的法线方向会随着表面形状的变化而变化,而且在一个连续表面上,相邻微区域的法线方向可能存在巨大的差异。这种不连续性会导致计算复杂度增加,并且需要考虑更多的特殊情况。半角向量很符合。
- 表面微区域的半角向量方向更直接地影响光线的反射:表面微区域的半角向量方向与光线方向的夹角可以更直接地影响光线的反射方向,而不需要考虑表面微区域的法线方向。因此,以半角向量为主的法线分布更加符合实际情况。
- 表面微区域的半角向量方向更加稳定:表面微区域的半角向量方向是相对稳定的,不会像法线方向那样随着表面形状的变化而剧烈变化。因此,以半角向量为主的法线分布更易于建模和计算,并且可以用较少的参数来描述微表面的性质。
- 更准确的反射模型:采用以半角向量为主的法线分布可以更准确地描述光线在表面微区域内的反射情况。在PBR中,光线的反射由BSDF(Bidirectional Scattering Distribution Function)描述,而BSDF中的F(Fresnel反射项)和G(几何遮挡项)都是以半角向量为主的,因此采用以半角向量为主的NDF可以更好地与F和G配合使用,得到更准确的反射模型。
- 计算简单:以半角向量为主的法线分布具有比较简单的数学形式,计算效率较高,适合实时渲染等应用场景。此外,还有一些基于半角向量的法线分布可以用一些预计算的LUT(Look Up Table)来进行快速计算,进一步提高计算效率。
总而言之,法向量是不稳定的,而半角向量可以给出微平面中整体的法线走向,尽管不是真正的垂直方向,但大致是对的。而且计算量简单,效果却非凡。
微平面的朝向方向与半角向量的方向越是一致,镜面反射的效果就越是强烈越是锐利。通过使用一个介于0到1之间的粗糙度参数,我们就能概略地估算微平面的取向情况了:

那么如何确定半角向量的比例是多少呢?NDF会返回在半角向量方向上的比例。比如给定半角向量$h$,如果微平面中有$35\%$
的比例是朝向$h$的,那么NDF就会返回0.35。半角向量方向上的比例越多,那么就越粗糙。现在业界内比较常用的NDF是Trowbridge-Reitz GGX:
其中$n$为法向量,$h$为半角向量,$\alpha$为粗糙度。下图是Trowbridge-Reitz GGX的分布图,其中x轴为$\alpha$,y轴为$\psi=\cos^{-1}(n\cdot h)$(即半角向量与法向量的夹角):

具体为什么Trowbridge-Reitz GGX长这样,挖个坑吧,以后有机会看看1975年的paper。
菲涅尔方程(Fresnel Function)
菲涅尔方程描述的是被反射的光线与被折射的光线的比例。这个比例会随着我们观察的角度不同而不同。在很多电介质都会体现这种特点,比如水就会有明显的折射现象。所以,这个方程简单来讲,就是补足一般渲染中没涉及到折射的部分而导致的能量不守恒问题。
菲涅尔方程本质其实非常复杂,这已经是物理光学的概念了,需要通过麦克斯韦电磁方程组来得到方程。由于本人学过工程光学,略知一二吧,所以这里给出简单的推导:
众所周知,光是一种电磁波,电磁波的形式在物理课我们都学过,电场强度$\vec{E}$和磁通强度$\vec{B}$相互垂直,两者的叉积得到的向量$\vec{k}$表示电磁波的传播方向。
在边界条件上,矩形区域极小,因此面积及侧面长度可以忽略,同时电场的切向分量在同一介质内可以认为不变。
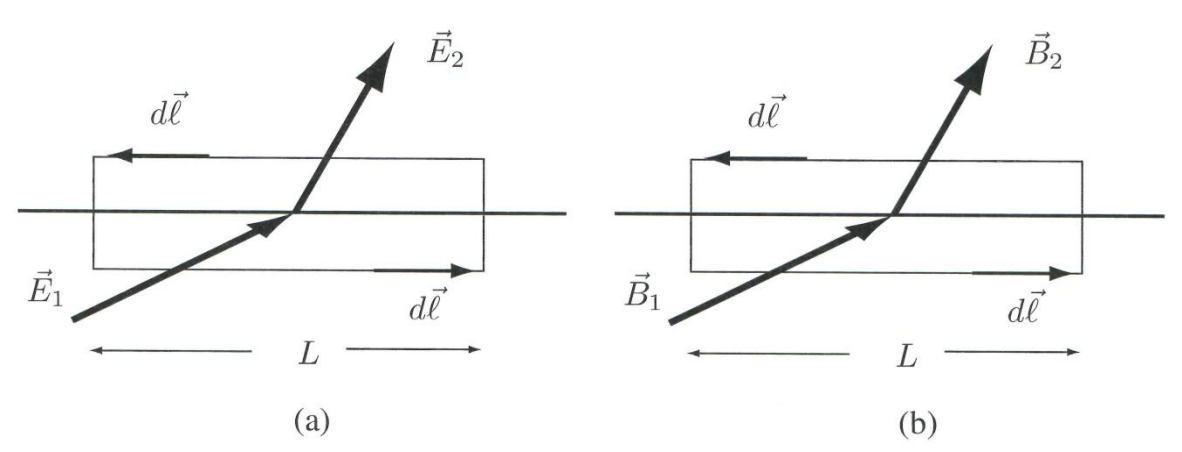
由麦克斯韦方程组,可以得到:
因此可以得到:
也就是说,电场的切向分量在边界上是连续的。同理,在非带电介质中,磁场的切向分量在边界上也是连续的:
对于边界上的电磁波,一般有:
根据边界条件,应该满足:
- 频率相同:$\omega_i=\omega_r=\omega_t$
- 相同坐标函数:$\vec{k_i}\cdot \vec{r}=\vec{k_r}\cdot \vec{r}=\vec{k_t}\cdot \vec{r}$,化简得到:$\theta_i=\theta_r,\ n_i\sin\theta_i=n_r\sin\theta_r$
- 连续边界:
入射光有两种入射方式,第一种是入射光偏振垂直于入射平面:
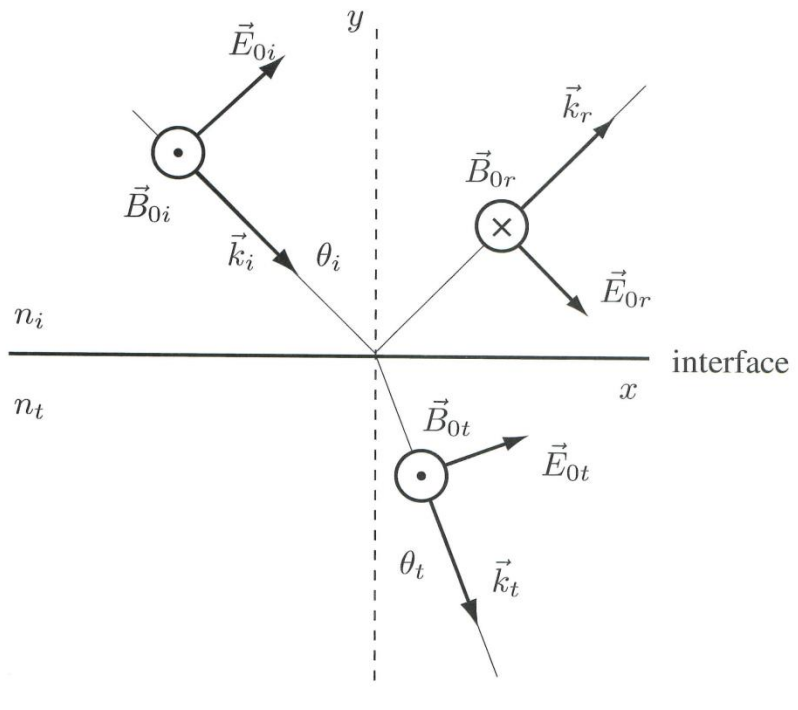
由边界条件可以分别得到:
电场:
磁场:
由
得
即:
由(1)(2),解得:
第二种是入射光偏振平行于入射平面:
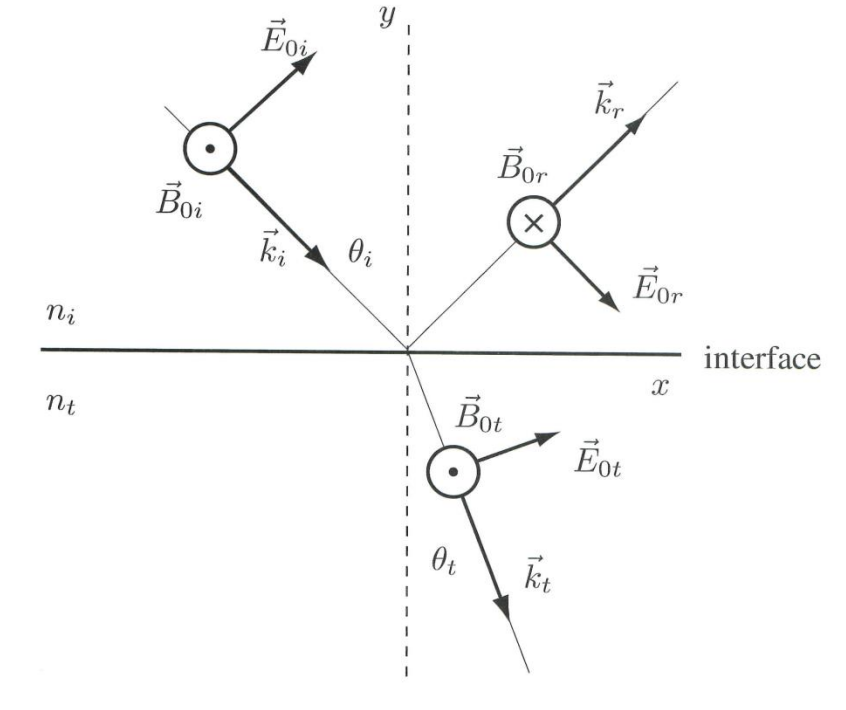
由边界条件:
电场
磁场
由于:
可以得到:
由(3)(4),可以得到:
综上所述,菲涅尔反射方程为:
忽略偏振光的影响,得到:
但这个方程也非常复杂,不好计算,但可以使用Shlick-Fresnel近似方程:
其中,$F_0$的取值可以不需要通过公式计算,而是参考下面的表格(Linear列),一般可以取0.03:
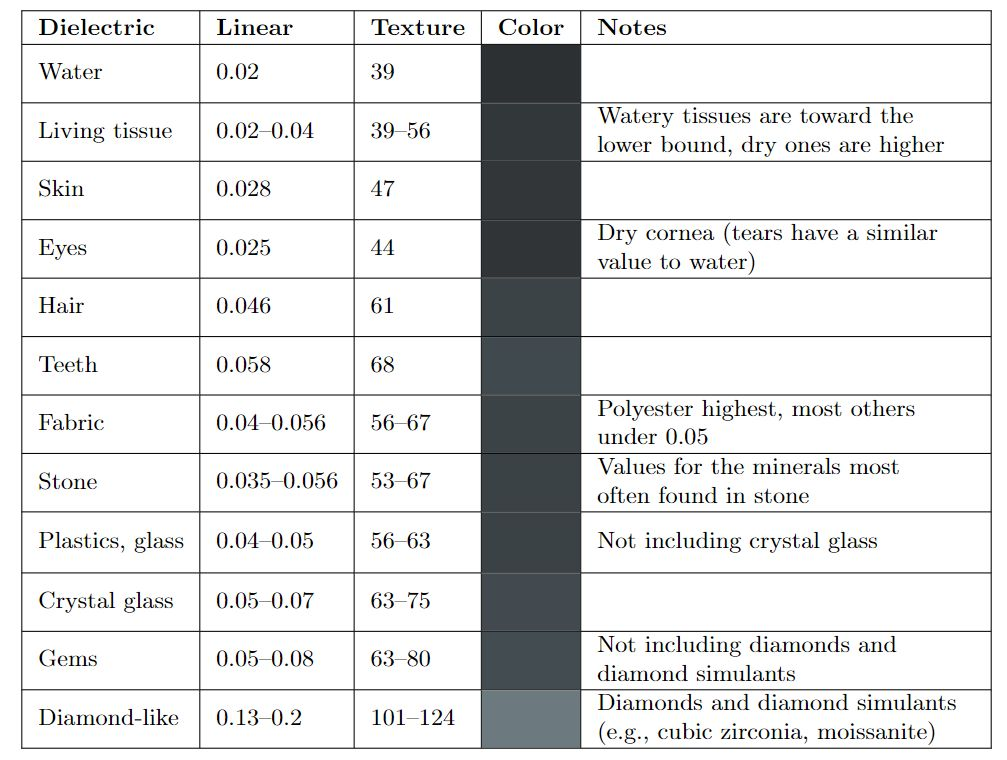
几何遮蔽函数(Geometry Function)
几何遮蔽函数描述的是光线被遮蔽衰减的效果:
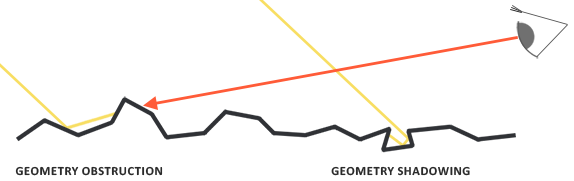
很容易知道,如果微平面的粗糙度大,那么就更容易有遮蔽衰减的效果。所以,几何遮蔽函数也可以跟NDF一样用粗糙度来描述,常用的是Schlick-GGX:
其中,$k$是$\alpha$的函数,有两种选择:
为了有效的估算几何部分,需要将观察方向(几何遮蔽(Geometry Obstruction))和光线方向向量(几何阴影(Geometry Shadowing))都考虑进去。我们可以使用史密斯法(Smith’s method)来把两者都纳入其中,获得一个较为精准的几何遮蔽函数:
PBR理论部分讲解完了,为了能在计算机跑,需要做优化:
渲染的时候后,我们使用metallic作为金属的比例,反照率albedo和金属的F0值,所以默认:
$mix(x,y,a)=x\times(1-a)+y\times a$
0.04是默认的电介质值,而由于菲涅尔项$F$本身带有镜面反射的比例,所以$k_s$可以去掉,而:
这是因为,$metallic$为1的时候,说明是金属,金属没有漫反射,所以$k_d=0$;如果是非金属,就要考虑这一项了。
最终反射方程:
其中$1-F$可以忽略:
1 |
|