辐射度量学与光线追踪原理
辐射度量学
背景
Phong和Blinn-Phong的经验模型过于经验,没有严谨的物理定义,所以计算机图形学急需要一个能够符合物理基本规律的光照知识,这就是辐射度量学提出的背景(基于物理光学)。
概念
- 辐射能$Q$,单位是焦耳,是能量,表示穿过一个曲面(类似于电磁学的高斯面)的光能。
辐射通量$\phi$,表示单位时间内穿过曲面的光能(注意是单位时间,辐射通量等价于功率)
立体角$\omega$(针对球面坐标系),类比于平面角(针对极坐标系):
可以得到立体角的公式:
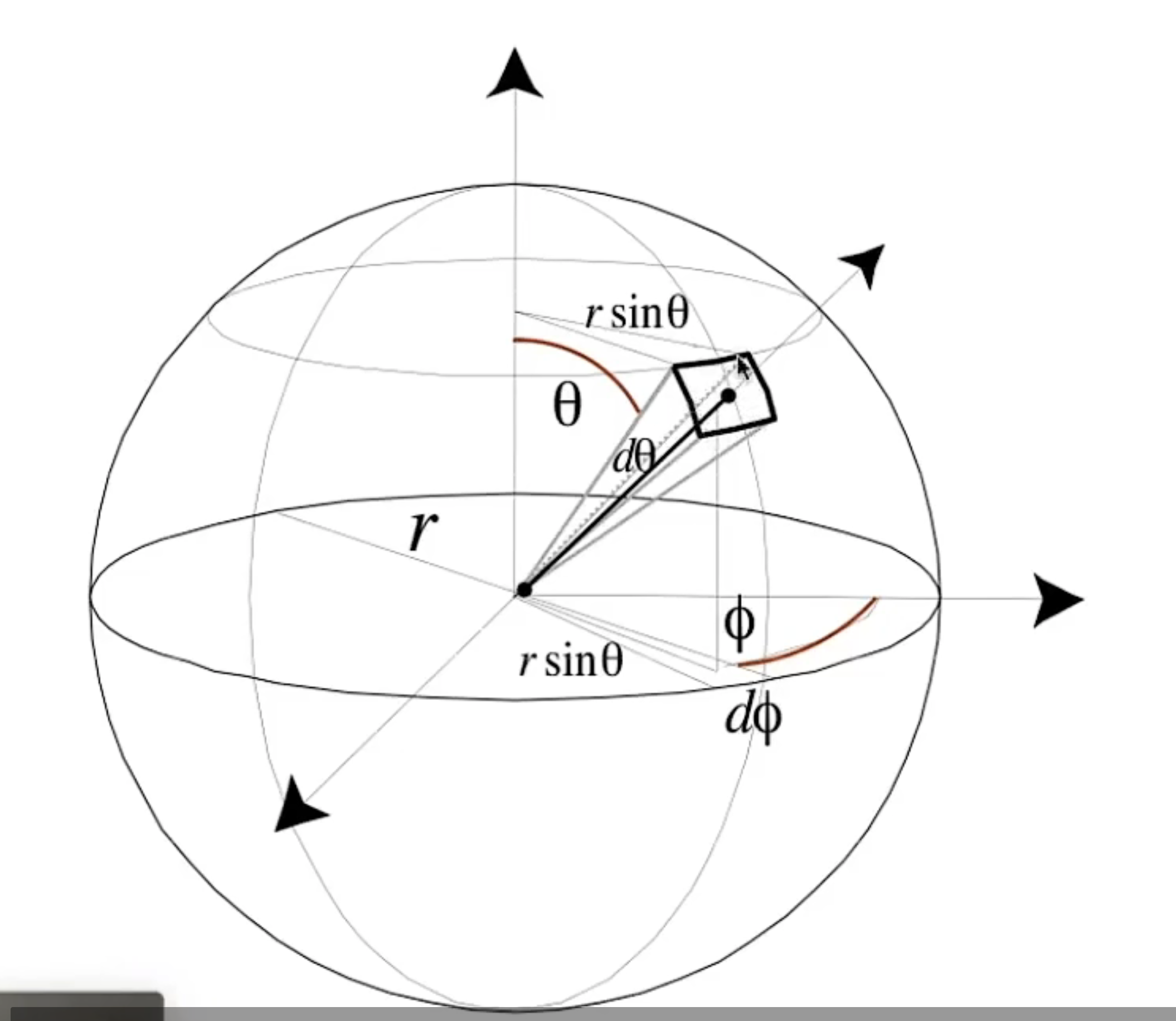
如上图所示,设球面上的单位面积为$dA$,那么可以算出(根据图):
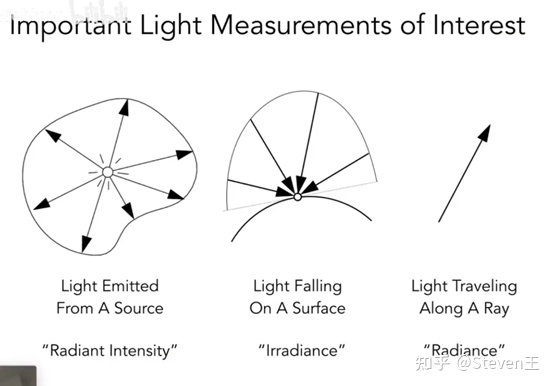
辐射强度$I$(Radiant Intensity),单位为cd(坎德拉),在光学中叫做光强。他表示单位立体角的辐射通量:
辐照度$E$(Irradiance),表示单位面积的辐射通量:
可以看出,这个量类似于我们在电磁学学到的磁通量定义公式:
所以,$E$可以表示一个球面(或者叫高斯面)上单位面积的接收到光强。那么$E$和$I$有什么区别呢?$E$表示的是一个球面上单位面积的接收到光强,而$I$表示的是一束光的光强而已。
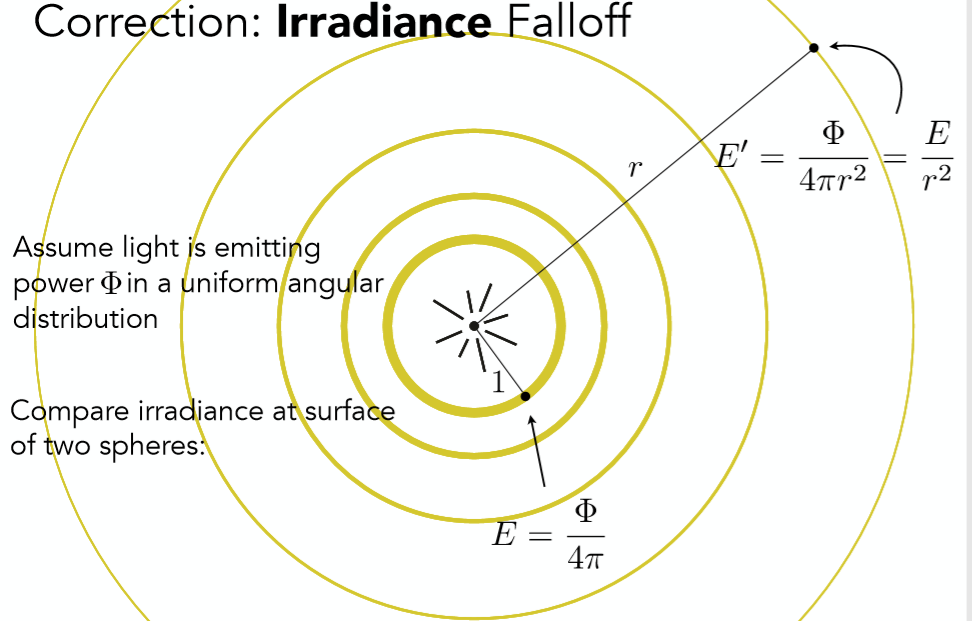
这个理论可以解释为什么在Phong模型中,光强按照平方阶次衰减。
如图,离光源最近的辐照度$E=\phi/4\pi$(半径为1),而距离光源为$r$的辐照度$E’=\phi/4\pi r^2=E/r^2$,所以两者的比值是$1/r^2$,这就证明了衰减是平方衰减。(可以看出来这里和电磁学非常相似,道理都是相通的)
辐射率$L$(Radiance),又叫光亮度。这是最常用(最重要)的一个物理量,也是构建渲染方程的主要物理量。他每表示单位立体角,每单位垂直面积的辐射通量。很像是Intensity和irradiance的结合。它同时指定了光的方向与照射到的表面所接受到的亮度。(就是这个单位面积在某个方向上吸收的光能)
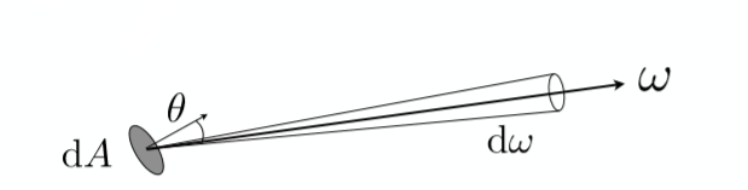
其中$\rm p$是入射点。
那么$L$和$E$的关系是啥呢?作如下变形:
这样进一步得到:
其中$H^2$是上半球。所以这个式子很好解释了Radiance是单位面积在某个方向上接受到的光强,而Irradiance是整个Radiance的求和(即所有方向上接收到的光强的总和)。
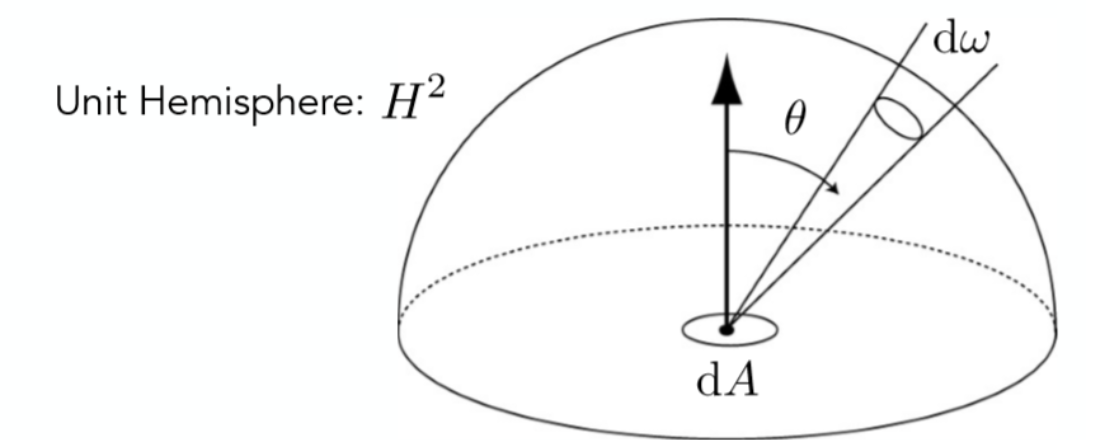
关于Radiance和Irradiance的理解:Radiance就表示该平面沿着某一个方向上吸收到的光能,这个微小发光面吸收到的所有能量之和就是Irradiance,等于所有Radiance的积分
BRDF函数(双向反射分布函数)和渲染方程
BRDF函数
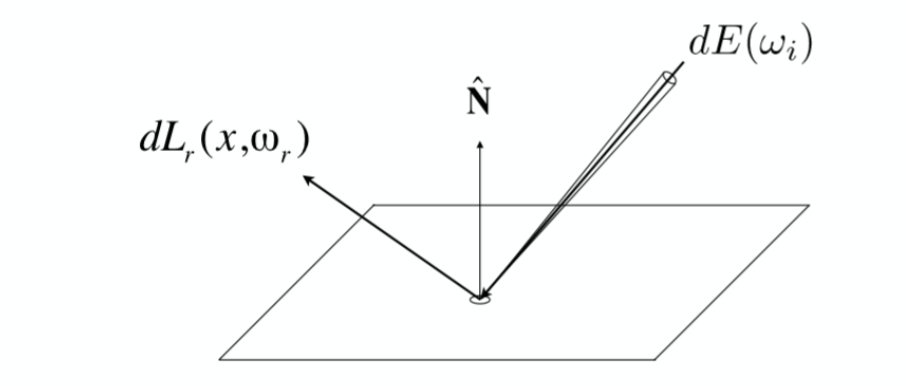
考虑一个位置为$x$的单位面积$dA$,接收到某个方向的光强$dE(\omega_i)$,经过材质的吸收能量后,反射出的光强为$dL_r(x,\omega_r)$,为了衡量反射出的光强与入射的光强的关系,类比于反射率的定义,我们定义一个函数来表示这个关系:
这个函数$f$,就是BRDF函数。因为这个函数的物理意义就是反射率,所以又叫做反射率函数。
因此,反射出的光强可以解出来是:
这就是反射方程。
考虑到物体还能自身发光,所以反射出的光强还包括物体自身的光强:
这就是渲染方程。
渲染方程的物理意义
渲染方程可以这样写:
大部份物理意义上面已经说过了,因为这里的积分其实本质是一种卷积,所以可以用算子来简化,这里讲解一下算子理解,为了简化方程,我们可以这样写一个方程大致表示渲染方程:
这是一种递归的写法,$L$为反射光强,$E$为光源光强,而$K$是反射算子(一种矩阵)。由线性代数的知识有:
由泰勒展开,有:
所以反射光强:
所以可以理解为,反射光强等于光源光强,加上光源经一次反射后的光强,加上光源经两次反射后的光强,以此类推。这就是真实的全局光照了。
蒙特卡诺积分
现在有了渲染方程,但如果直接数值方法计算定积分,效率太低了。所以引入概率学的蒙特卡诺方法,类似于几何概型。
蒙特卡诺积分
蒙特卡诺方法会将:
以概率的角度,求出他的近似值。
考虑一个函数图像:
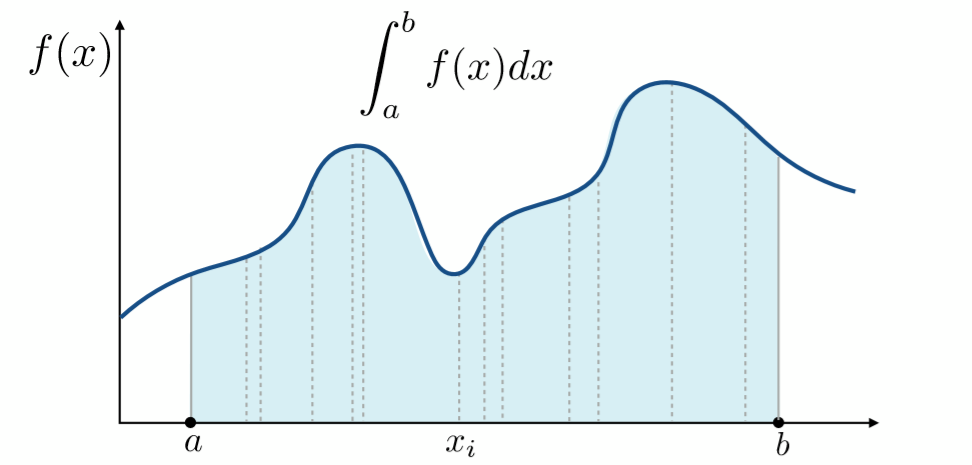
选定一个随机变量$X_i\sim P(x)$,遵循某种分布$P(x)$。从这个分布随机挑选出一个值$x_i\in X_i\in[a,b]$,因为这个集合关系,所以就会导致$P(x_i)$的范围为:
所以$1/P(x_i)$决定了矩形的宽度,可以用来计算矩形面积。
然后取$f(x_i)$作为矩形的高度,然后计算矩形面积:
重复$N$次,最后取算术平均数,就是这个积分的近似值了(是不是很像几何概型):
于是:
如果我们采用均匀分布$X_i\sim U(a,b)$,就有$P(x_i)\equiv1/(b-a)$,这个时候每次的获取的矩形面积的宽度都是$(b-a)$,于是每次随机计算出的矩形面积为:
于是:
证明蒙特卡诺积分的正确性
因为蒙特卡诺是概率模型,我们计算数学期望,如果值就是积分本身,那么这个模型就是正确的:
证明完毕
光线追踪
由蒙特卡诺积分,可以化简渲染方程为:
所以我们可以用递归来计算路径追踪(暂时忽略自身光):
1 | shade(p,wo): |
这是最简单的路径追踪,但没有解决递归边界和多物体的问题(比如下面就是P的光线还射到了物体Q):
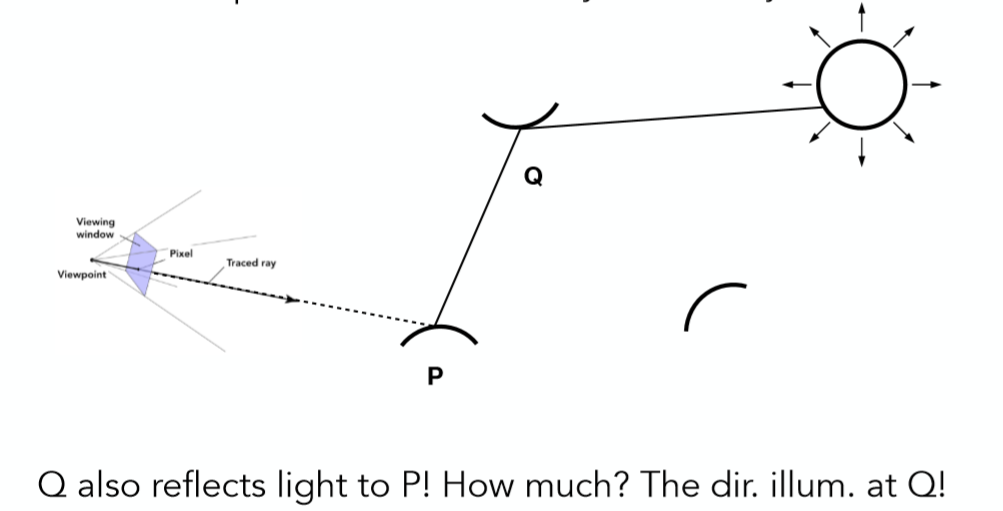
另外,我们希望选取一个方向的随机光线,因为多个方向会有产生指数级别的光线,这是重量级的。
1 | shade(p,wo): |
但由于只射出来一条光线,误差非常大,万一没击中任何东西呢?所以我们要连续发射一条光线,不断地发射,这样就有n个路径,然后求平均,这样就精准多了:
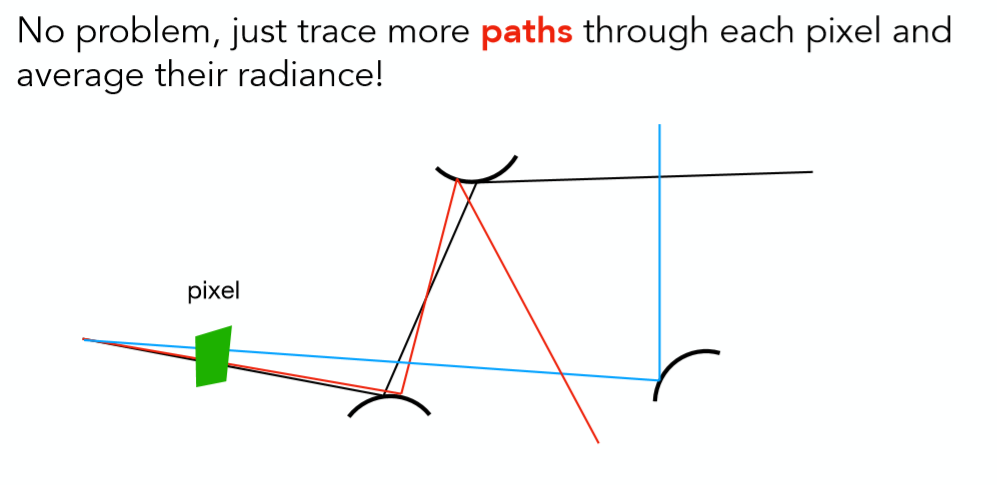
1 | ray_generation(camPos, pixel): |
最后因为shade函数没有递归边界,所以利用俄罗斯轮盘赌方法(也就是设定一个概率阈值,超过就返回):
1 | shade(p,wo): |
最后一个小问题如下:

可以发现,当光源特别小的时候,光线很难去追踪。可以采用逆向思维解决,从光源追踪就可以。
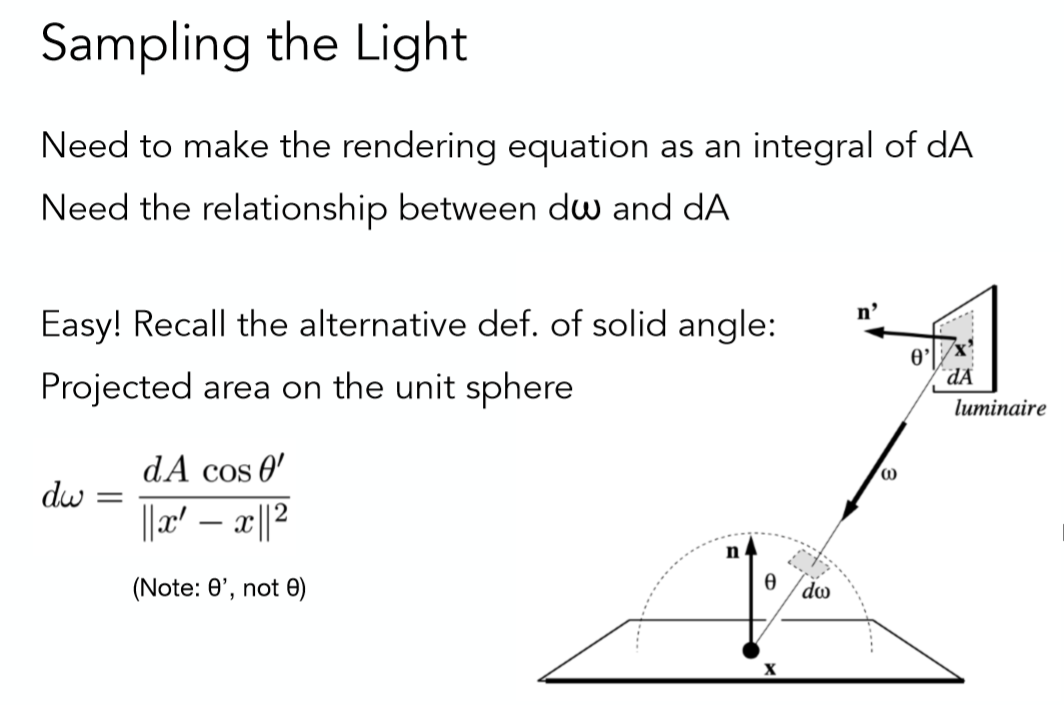
我们只需要将渲染方程对立体角的积分转换到为光源单位面积的积分就好了,也就是说找到$dA$与$d\omega_i$的关系。(立体角本质也是面积的,相对于半径平方的面积)
所以反射方程改写为:
最终伪代码:
1 | shade(p, wo) |

上面的代码都是基于面光源而设定的。