OpenGL教程:8. 摄像机坐标系
摄像机方向
摄像机是一种抽象的结构,它表示我们看东西的媒介,类似于眼睛。为了定义摄像机,我们给定摄像机的世界空间位置向量$\boldsymbol{eye}=(x_0,y_0,z_0,1)$,以及我们要观察的片元的世界空间位置向量$\boldsymbol{frag}$。
为了构建摄像机的坐标系,我们需要三个正交的基向量,而其中一个必须表示方向信息。首先可以计算出摄像机的方向向量:
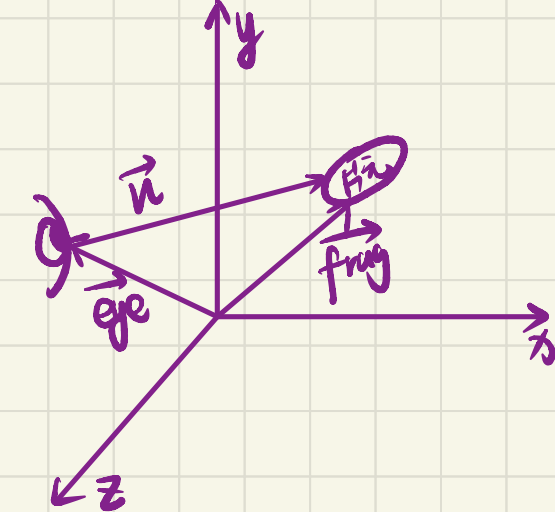
可以计算摄像机的视角方向向量,简称方向向量:
摄像机的右轴
现在有了第一个基向量$\boldsymbol{n}$,然后需要找到摄像机的右轴,充当其坐标系的第二个基向量。为此,我们要引用一个辅助向量$\boldsymbol{up}=(0,1,0)$,也就是上向量。进行叉乘,就可以得到第二个正交的基向量:
如图所示:
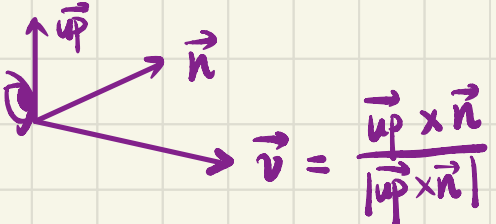
摄像机的上轴
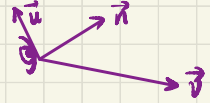
最后处理上轴,请问上轴是$\boldsymbol{up}$吗?不是!因为$\boldsymbol{up}$不一定与$\boldsymbol{n}$正交,因此我们还要找到上轴基向量!
非常简单,只需要:
如图所示:
LookAt矩阵的推导
为了实现世界空间与观察空间的变换,我们需要引入一个矩阵。这就是LookAt矩阵的作用。
LookAt矩阵实现了将摄像机坐标系的基向量变换到世界坐标系的基向量。为此我们将进行推导。我们令:
其中$\boldsymbol{T}$是平移矩阵,$\boldsymbol{R}$是旋转矩阵。这个矩阵将进行摄像机坐标系基向量变换到世界坐标系基向量。
首先需要将摄像机平移到世界坐标原点,也就是将$\boldsymbol{eye}$向量平移到原点位置,不难知道平移矩阵的值:
因此:
平移到了原点。
接下来推导$\boldsymbol{R}$,$\boldsymbol{R}$是将摄像机坐标系的基向量旋转到世界坐标系的基向量的位置,即:
其中$\boldsymbol{\alpha=}\left[
\begin{array}{cccc}
0&0&0&1
\end{array}
\right]^T$。
但这样比较难计算,我们可以求$\boldsymbol{R^{-1}}$然后求逆矩阵就好了!也就是将世界坐标系的基向量变换到摄像机坐标系的基向量:
根据格拉姆-施密特正交化的理念,能够知道$\boldsymbol{R^{-1}}$是正交矩阵,转置矩阵等于逆矩阵,因此:
综上所述:
OpenGL教程:8. 摄像机坐标系
http://blog.inverseda.top/2022/11/07/ComputerGraphics/OpenGL/8.摄像机及其坐标系/
Comments
Your browser is out-of-date!
Update your browser to view this website correctly.&npsb;Update my browser now