OpenGL教程:7. MVP变换
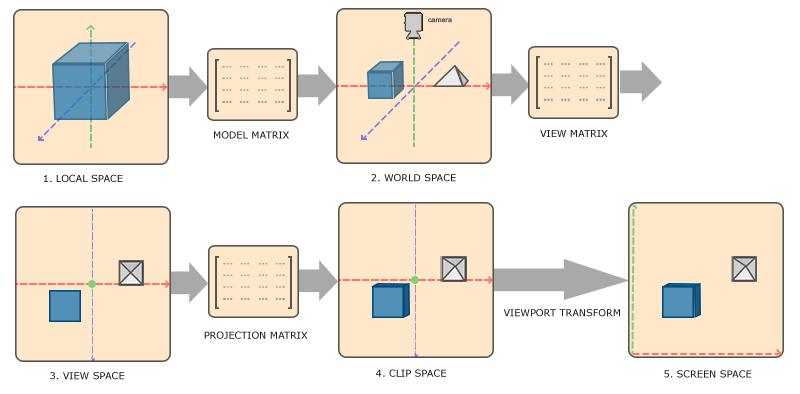
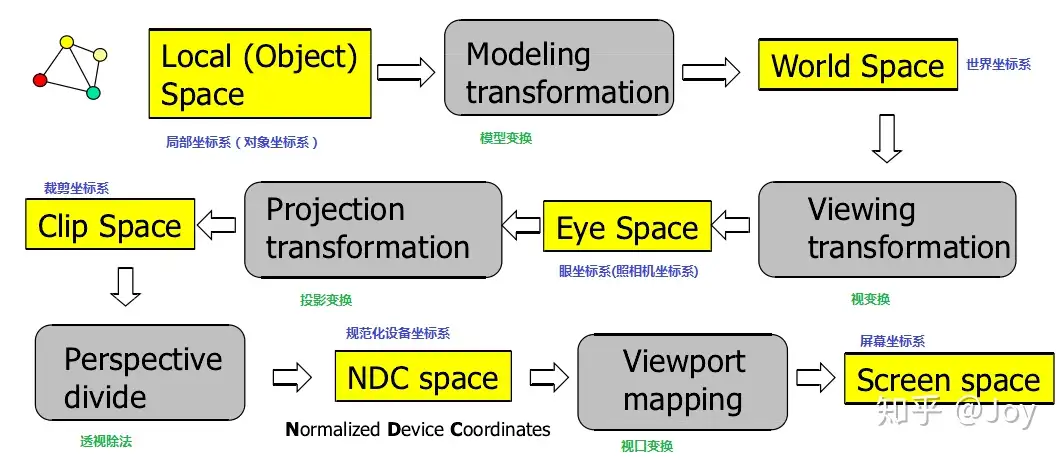
初始阶段,我们在Local Space中,我们为了能够让屏幕显示3D的效果,需要进行MVP变换。
迄今为止,我们渲染2D图形,我们现在准备利用MVP变换,让我们的屏幕能显示3D世界。
首先是Model Matrix,将本地的空间中的物体渲染到World Space世界空间中,这个世界空间是所有物体所处的位置!(在最初的坐标系中,范围只有$(-1.0,1.0)^3$,通过Model矩阵将范围扩充到$\boldsymbol{R}^3$)
然后获取相机的方向信息,得到View Matrix,乘以后就知道以相机为方向的视角了。
接下来是Projection Matrix投影,让物体真正的拥有3D效果,一般使用透视矩阵。
然后经过透视除法以及视口变换,就转换到了Screen Space了。
最后就成功在Screen Space显示三维物体了。这就是MVP变换,用数学表达式解释:
将本地的坐标$\boldsymbol{Position}$进行矩阵变换,得到屏幕坐标下的坐标$\boldsymbol{glPosition}$
齐次坐标表示
在三维坐标系中,我们使用
的位置向量表示一个位置信息。
但这其实对于矩阵变换来说特别不方便,主要在于对于坐标的平移操作:
但是这样操作很不好,毕竟有加法,有没有一种矩阵能够一次性平移呢?我们如果将坐标转为齐次坐标:
那么:
我们只用了一个$4\times4$的矩阵实现了平移操作。因此,我们的矩阵操作都是基于齐次坐标!
局部空间 Local Space
我们的物体对象最初在局部空间。也就是如果没进行任何变换,那么空间都处于这个位置。一般来讲,坐标都为$(0,0,0)$。所以我们需要将物体摆放到任意位置的时候,就应该进行线性变换了!
世界空间 World Space
我们需要将物体摆放到世界中的任意位置,就得让物体的坐标进行模型变换,即物体的坐标乘以矩阵Model Matrix。
Model Matrix的主要工作是将局部空间坐标系转成世界空间坐标系。说白了就是平移坐标,因此Model Matrix的本质就是平移矩阵:
于是,这里将局部空间变换成世界空间,只需要:
观察空间 View Space
观察空间也叫摄像机空间,是以图形学中的摄像机模型为视角的一个空间。通常需要一定的位移和旋转变换才能得到。这交给View Matrix解决,通常下会采用LookAt矩阵来代替View Matrix。
View Matrix的主要工作是转换到摄像机的视角。摄像机的视角矩阵我们使用LookAt矩阵实现的,具体推导可以看摄像机及其坐标系的文章,这里只给出矩阵的具体形式:
其中$\boldsymbol{u, v, n}$是摄像机坐标系的三个基向量,$\boldsymbol{eye}$是摄像机的位置向量。LookAt矩阵的作用是用来处理将观察空间的基向量$\boldsymbol{u, v, n}$转换成世界空间的基向量$\boldsymbol{x, y, z}$。
裁剪空间 Clip Space
通过前面的变换,我们来到了观察空间。但有个问题是,窗口显示不了那么大的区域。因为窗口时有尺寸的。所以我们需要把一些画面给裁剪掉,这就是裁剪空间的由来。裁剪空间的变换,我们需要用到投影矩阵,也就是Projection Matrix。一般投影的方式有两种:正射投影和透视投影。
正射投影
顾名思义,其实就是将物体原有的投影原封不动的投影到坐标面:
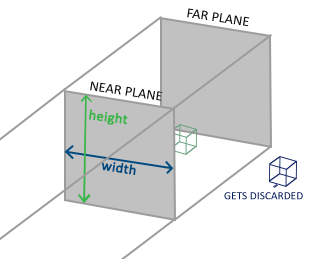
但这样做会产生不真实的效果。若要采用更真实的效果,应当采用透视投影。
透视投影

这就是透视投影,会出现近大远小的情况。我们采用透视投影矩阵完成这样的效果。其实不难做到,我们可以看出来,最终的输出应当为:
Comments
Your browser is out-of-date!
Update your browser to view this website correctly.&npsb;Update my browser now