电磁场理论基础
磁场
何为磁感应强度?为什么不叫磁场强度?
这其实是个历史问题。最先确实引入了磁场强度$\vec{H}$,但后来发现磁场强度这个物理量无法解释很多电磁现象。所以我们为了方便研究磁场,导出了磁感应强度$\vec{B}$。研究表明:
这是磁感应强度和磁场强度的对应关系。
而在高中,我们更多是使用磁感应强度这个物理量。与之对应的电场强度$\vec{E}$。
磁感应强度
我们在研究带电粒子在磁场的运动特征,发现粒子所受的磁场力(后发现叫做洛伦兹力)与速度、正负、和另外一种量有关系。我们把这个量定义为磁感应强度$\vec{B}$,显然它为向量。
我们规定,正电荷$+q$以速度$\vec{v}$在磁场某点,若不受磁场力的作用,则此时速度的方向就是磁感应强度的方向。
研究表明,电荷速度积$q\vec{v}$与磁感应强度$\vec{B}$,总是成一定的关系的,后来计算出:
这就是我们要学习的洛伦兹力在垂直的时候的公式。
这就是磁感强度。
洛伦兹力—单个电荷在磁场中受到的磁场力
磁场力$\vec{f}$即与运动电荷速度$\vec{v}$垂直,又与$\vec{B}$垂直,所以他们三个构成了右手螺旋关系(三维空间的向量概念):
这是洛伦兹力的矢量式,写成大小:
其中$\theta$是$\vec{v}$和$\vec{B}$的向量夹角。
这就是洛伦兹力,它有以下特点:
- 洛伦兹力在单个磁场作用电荷的时候,速度与磁感强度永远垂直,这就意味着洛伦兹力永不做功。而且不参与能量转换。
- 受到洛伦兹力的电荷在磁场中做匀速圆周运动,满足向心力定理。
接下来我们来讨论电荷在磁场的运动特征:
洛伦兹力充当圆周运动的向心力
可以解出:
写成动量形式:
这就是速度和动量。
由于匀速圆周运动的周期为:
根据时间成比例的性质,可以求出电荷在磁场运动的时间:
洛伦兹力的方向可由左手定则确定,左手定则是指磁感线穿掌心,四指指向运动方向,而大拇指就是洛伦兹力方向。
安培力—洛伦兹力求和后的结果
考虑一个导线在磁场。导线本身没有什么磁作用,但是导线里存在电流,也就是存在自由电荷。所以我们说这些自由电荷都可以受到洛伦兹力,这样这么多的电荷给导线的作用,使得导线受到了电荷的作用力,这种力就是洛伦兹力的合力,也叫做安培力:
我们证明:
于是得出安培力的计算式
向量式
需要注意的是,$I\vec{L}$是一个整体,他表示的是电流元向量。这说明其实标量和矢量很多时候也是可以人为强制定义,比如面积本身是标量,可某些时候就是要让成为向量,在磁通量的学习就可以知道了:$\vec{S}=\vec{n}S$。
安培力也可由左手定则确定,磁感线穿掌心,四指指向电流方向,大拇指就是安培力的方向。(他为什么和洛伦兹力的法则那么像?)
对于曲线段的导线,由于长度$L$是会变化的,因此我们用积分:
故
所以得出,不管是哪种样子的导线,最后等价于起始点和终点连线段的安培力。
带电粒子在匀强磁场的运动——匀速圆周运动
根据前面的结论可以知道,带电粒子在匀强磁场是做匀速圆周运动的。所以根据洛伦兹力充当向心力,可以得到:
具体思路是:
- 定圆心
- 找半径
- 根据题意列出方程解
虽然步骤简单,但实际上我们遇到的题可能会非常复杂。但其实只要做到前面两点,就可以得到很多分数(步骤分),因此也是非常赚的。现在我们来分别讨论这三个步骤:
定圆心
根据圆的几何知识,我们可以知道:在轨迹中任选两点,这两点的中垂线一定经过圆心。于是就有了第一种确定圆心的方法,首先在轨迹中找到两个点:

我们看出,其实只要知道两个点的弦,以及知道其中一个点的力线或者速度线,就可以得到圆心。
所以这个方法适用于我们不知道粒子的运动方向,但是知道粒子运动过程中有经过AB两个点。
另外一种方法就是知道粒子的运动方向,那就可以大胆的利用两个力线相交即为圆心的原理来求出圆心的位置:

找半径
半径首先分为两种半径:磁场半径和几何半径。这两个半径的值都是相等的,但方程的表达形式不一样:
首先求出半径用这两种办法都可以,就看题目的意思了(很多时候只能求几何半径)
我们可以利用两个半径的联立求出诸如$q、B、m$等未知量,具体步骤为:
- 求出几何半径和磁场半径
- 联立两个方程,会得到关于$q、B、m$等未知量的方程,然后根据题意代入求解
这些步骤实行起来一般来说是十分简单的。
电磁场综合应用——压轴题常考
正交电磁场
正交电磁场的概念是匀强电场和匀强磁场正交,也就是$\vec{B}⊥\vec{E}$,所以磁场和电场要垂直。
特殊情况下,当:
即
此时粒子在这个正交电磁场做匀速直线运动。所以可以通过粒子的运动判断这个电场和磁场的关系是否满足上面的方程式。
一般地,电场和磁场都有这样的关系:
所以当电磁场不正交,就有:
复合场的综合应用
我们更多的是见到复合场,即要么电磁场结合在一起,要么分开。但粒子都会在这两个场运动,观察众多题目可以得到这样的规律:
一般而言,粒子首先在电场进行加速,加速后进入磁场,然后据此根据题意分析运动情况就好。
而在电场加速的时候,可能会做匀加速直线,但更多的应该是类平抛运动加速,这需要你能够好好掌握前面所学的内容。
整体思路为:
在电场中,无论是什么运动都有:(动能定理)
或者
通过这两个方程任选其一(根据题目给的条件选方程),然后就可以得到进入磁场的速度。然后利用前面所学的知识求解即可。
电场中,若做匀加速直线运动,那么直接用动能定理即可。
若做类平抛运动,可能要结合平抛运动的知识来做:
根据这三个基本的类平抛方程,可以求出基本解:
当然,也有很重要的结论:
其中$\theta$为速度角,$\alpha$为位移角。
当然,类平抛运动也可以根据动能定理来求解。这里就不再赘叙,按照做功分析就行。
电场理论进阶
库伦定律
库仑定律指出,两个电荷之间存在相互作用,即:
其中
所以这和高中稍微有些差别,但这个差别是必要的。
$k$为静电力常量,这是高中见到的。但其实这个量很少用,用的更多的反而是后面的量。其中$\epsilon_0 $是真空电容率,其值$\epsilon_0=8.85\times10^{-12}F·m^{-1}$。$\vec{e_r}$为$q_1$到$q_2$的单位矢量,$|\vec{e_r}|=1$,这就意味着库仑力也是矢量。至于为什么$\epsilon_0 $用的更多?之后你就会体会到了。
点电荷的电场强度
根据库仑定律,以及电场强度的知识,不难得到:
这就是点电荷的电场强度公式,由于等式右边也有个单位矢量,故电场强度也是一个矢量。如果$Q>0$,则整个向量式都是大于0的,由此正电荷可以知道$\vec{E}$与$\vec{e_r}$的方向一样。反之相反。
电场强度叠加原理
由于电场强度为矢量,则它符合叠加原理。这个叠加原理遵循向量的平行四边形法则,即:
但这是向量的相加!不是标量!所以你不可以直接把他们的数值相加!他们是有一定的角度的!有离散型和连续型的叠加原理。
进而推广$n$个电场强度相加的数学表达式:
但注意到这个是离散型的电场强度叠加原理。万一我们要求不规则带电体激发的电场强度呢?
我们假设这个带电体的体积为$V$,在带电体上取一个微小的电荷$dq$,其线度对于$V$可谓是无穷小,因此$dq$在某点$P$激发的电场强度为:
那么进行积分,就可以得到:
这就是连续型电场强度叠加原理。
特别地,如果我们知道这个带电体的密度$ρ$,那么就有$dq=ρdV$,就可以化为体积积分。
体积积分可以用三重积分计算方法做。但实际计算的时候,很少用到这种方法(因为遇到的都是简单的)。
电场强度通量
类比于磁通量,其实也有电通量的东西,记作$\Phi_e$,其实你也应该能猜出结果:
其中$\vec{S}=\vec{e_r}S$,$\vec{e_r}$依然为单位矢量。
对于曲面来说,有时候面积不好求,同样利用积分也可以解决。我们求曲面积分即可:
设微小的电通量$d\phi_e$,那么就有:
那么积分就有:
这个结果将引入麦克斯韦方程组的第一个方程:高斯定理。这是最重要的定理。
高斯定理
我们前面学得,一个球体电荷在外面激发的电场强度为:
取球面的一个面积元$dS$,有:
于是通过整个球面的电场强度通量为:
由于球面的表面积为$S=4\pi R^2$,那么代入得到:
这就是高斯定理。通过实验证明,这个式子不仅适用于球面,对于任何一个闭合曲面都适用。
最后得到
说明通过该闭合曲面的电通量等于该闭合曲面内的电荷量之和除以真空电容率。
电位移—一个不在真空情况下的电场强度
当环境不在真空的时候,电场强度就不再是电场强度了。换言之,我们应该引入电位移这个矢量,作为电场强度的替补,用$\vec{D}$表示:
其中$\epsilon_0$为真空电容率,$\epsilon_r$为当前环境的电容率,令$\epsilon=\epsilon_0\epsilon_r$,因此可以改写上面的高斯定理:
这就是真正的麦克斯韦方程组的第一式:高斯定理。
静电场的环路定理和电势能
回到真空环境。
我们在高中的学习知道了,静电场是一种保守场,所以环路上做功为0,那么稍微推广下,就可以得到曲线积分:
这是因为电场力做功为:
绕了一圈回来,就是环路,回到起点做功是为0的,所以就有上上面的式子。
当不是环路积分的时候,那么就有:
所以电势能就出现了,定义为:
电势与高中做功公式的推导
电势定义为$V$(这次就不是$\phi$了,要区分)
所以就有:
所以某A点电势,就等于正电荷从无穷远处到$A$点处静电力做的功。(这与高中的定义相同)
电势差:
这说明静电场中AB两点电势差,就等于正电荷从点A到点B静电力做的功。
由此就有了万能的公式:
就是这样推导出来的。
对于匀强电场的做功推导:
这就是我们高中常用的两个电场力做功公式。
电势的叠加原理
电势由于是标量,所以叠加原理就是代数和,首先是离散型电势叠加原理:
总结为:
对于连续型电势叠加,我们同样采用积分:
电场强度与电势的关系
理论表明,电场强度为电势梯度的负值:
写成你能够理解的式子,就是
也就是电场强度为电势的方向导数,简单解释一下什么是方向导数:
我们平时的导数是对x求导,那么就记作$dy/dx$,那如果是对一个方向的路径求导呢?那么就是$dy/dl$,$l$为路径。所以方向导数实际上是统一了求导的情况,不止是对x求导了。
这里$dV/dl$就是对这个$l$路径求导数,本质也是一样。所以也有对x求导数的情况。
但毕竟是路径。不如对xyz求导数方便啊!那怎么办呢?当然是将这个方向导数想办法转换到xyz的方向分别求导。
所以就有了梯度向量的概念,记作$\vec{gradf}$或者$\nabla f$:
(函数f为三元函数)
而方向导数就是梯度向量的模:
其中$\alpha、\beta、\gamma$是梯度向量的方向角,分别是x、y、z方向。
所以电场强度的电势表示又可写成:
当然,这是三维情况下的电场强度的电势表达。但高中我们只接触二维的情况,那么就有:
所以这就是我们在题目中常见的$ V- x$(高中为$\phi - x$图像)图像实质斜率,它的斜率为$-E$,表示电场强度的负方向。这样又回到了高中。
在高中我们是这样推导二维情况下电场强度的电势表示:
令$E_{pA}=qV_0$,知道:
即
可以知道在$l$方向上,$V-l$的斜率为$-E$。所以分析的时候看图像中斜率的变化即可。尽管得到的结果是正确的,但这个推导十分不严谨。所以还是得学习微积分才能懂得实质。
现在我们知道电场强度为电势梯度的负值了!
简谐运动
表达式的推导
考虑一个弹簧振子和物块,他们均处于光滑的水平面上,根据牛顿第二定律,有:
令$\omega=\sqrt{k/m}$,则
这是一个齐次的二阶线性微分方程,可以简写成
它的特征方程为:
解出
这是一对共轭复数根,因此根据欧拉公式,可以解出$x$关于$t$的函数:
令$A=\sqrt{C_1^2+C_2^2}$,得到最终的方程
x-t图像分析以及常用结论
由上述推导可以知道,x-t是一条正弦函数曲线。满足周期性。因此存在周期的性质,我们现在来进行分析:
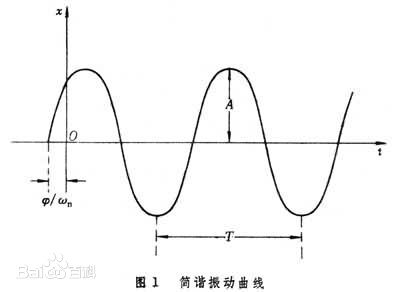
根据表达式,可以知道:
这就是简谐运动的周期表达式,具有一般性。任何一种简谐运动都可以用这个表示其周期。
单摆运动-一种简谐运动
考虑一个单摆锤,它是一个球体
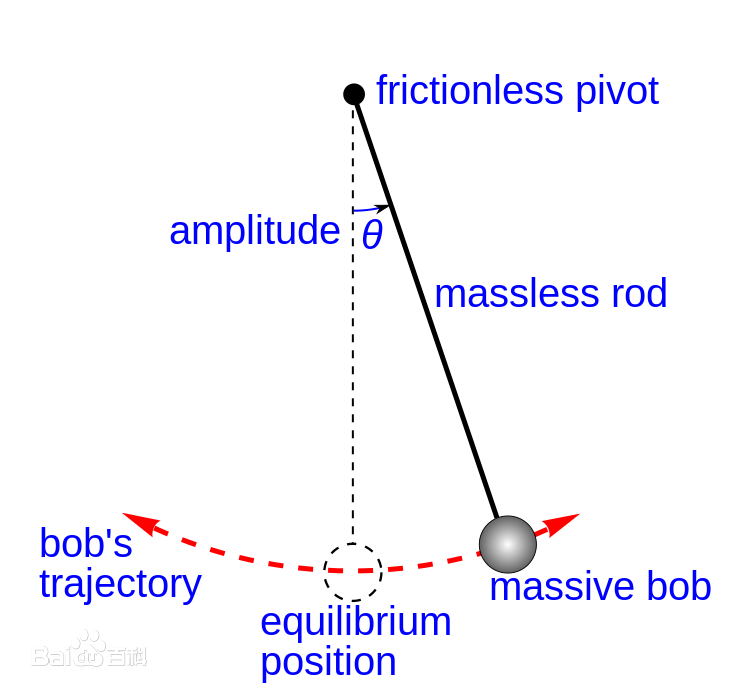
受力分析,可以求出切向力关系:
我们认为当$\theta\rightarrow0$的时候,近似$\sin\theta=\theta$
因$\theta=\frac{x}{l}$,因此
这是因为:
当$\theta$很小的时候,后面可以忽略不计。
单摆运动也具有周期,因为它是简谐运动,那么:
由于$F_{切}=-kx$(简谐运动应满足的方程),由此
代入
这就是单摆的周期公式