KMP算法
next数组计算方法如下
默认next[0]=-1,字符串从0出发。
计算的方法是:
1 | int j = 0, k = -1; |
其中p是模式串。
接下来我们来推导KMP的状态转移方程。
设$dp[j]$是第j处最大公共真前后缀的长度,那么如果$p[j]==p[k]$,那必然有$dp[j+1]=dp[j]+1=k+1$(可以想象一下,后面一位字符也是相等的,那就说明这里的最大公共真前后缀的长度等于前一位的+1嘛!),并且j和k都递增一次。
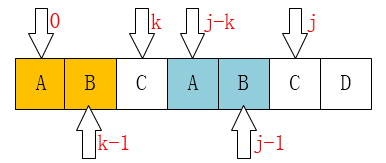
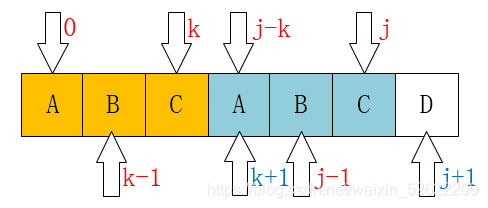
如果$p[j]\ne p[k]$,如图:
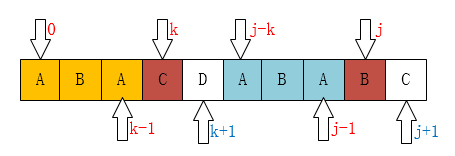
虽然我们知道$dp[j]=k$(在图中k为3,说明j处的最长公共前后缀的长度是3),但是当指向$j+1$的时候,可以看到公共的前后缀变成了AB,显然AB的长度为2,这个值刚好为$dp[k]+1$,因此此时$dp[j+1]=dp[k]+1$,并且k应当回溯,因为j往后的字符串很有可能和$dp[k]$前的字符串相匹配,如果不回溯就会找不到后面的最长公共前后缀了!
其中$dp[0]=-1, dp[1]=0$。并且只有$p[j]=p[k]$的时候,$k,j$指针都向右边移动。当$ p[j] \ne p[k]$的时候,我们是将k进行回溯了,即$k=dp[k]+1$,并且j向右边移动。因此有一种更笼统的写法:
这个版本更适合用于循环,表达非常简单!既然状态转移方程找到了,我们就该写循环主体了:
首先,字符串从0开始,一般规定$dp[0]=-1$:
1 | int k = -1, j = 0; |
Comments
Your browser is out-of-date!
Update your browser to view this website correctly.&npsb;Update my browser now