单调队列稍有不同,需要用到双端队列模拟。不然的话无法正常满足单调性。
并且双端队列最好自己手写,用c++的dequeue效率非常慢,很容易tle的。
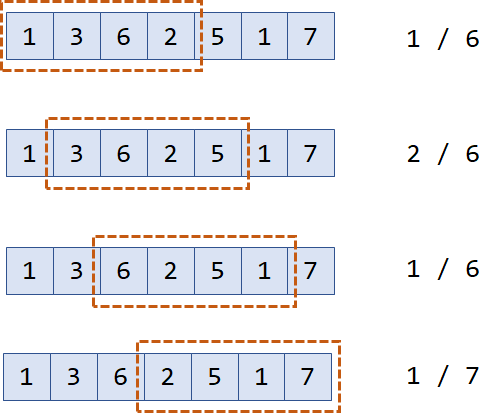
单调队列常用于解决连续k个数中的操作,比如滑动窗口问题。
给定一个大小为 $n≤10^6$ 的数组。
有一个大小为 k 的滑动窗口,它从数组的最左边移动到最右边。
你只能在窗口中看到 k 个数字。
每次滑动窗口向右移动一个位置。
以下是一个例子:
该数组为 [1 3 -1 -3 5 3 6 7],k 为 3。
你的任务是确定滑动窗口位于每个位置时,窗口中的最大值和最小值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| #include <iostream>
using namespace std;
const int N = 1000010;
int a[N], q[N], n, k;
int front = 0, tail = -1;
int main() {
scanf("%d%d", &n, &k);
for (int i = 0; i < n; i++) scanf("%d", &a[i]);
for (int i = 0; i < n; i++) {
if (front <= tail && i - k + 1 > q[front]) front++;
while (front <= tail && a[i] <= a[q[tail]]) tail--;
q[++tail] = i;
if (i >= k - 1) printf("%d ", a[q[front]]);
}
printf("\n");
front = 0, tail = -1;
for (int i = 0; i < n; i++) {
if (front <= tail && i - k + 1 > q[front]) front++;
while (front <= tail && a[i] >= a[q[tail]]) tail--;
q[++tail] = i;
if (i >= k - 1) printf("%d ", a[q[front]]);
}
}
|
